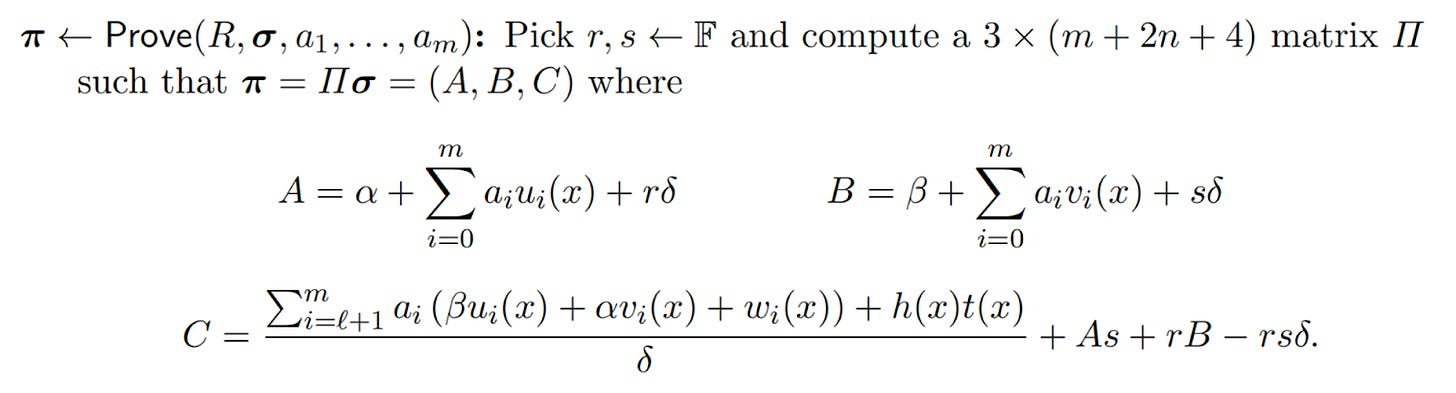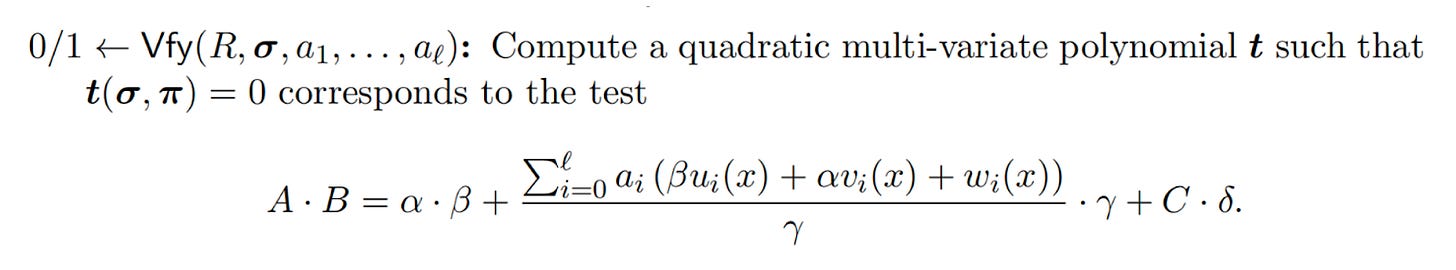Welcome back to Full Stack!
‘Zero-Knowledge’, or what’s commonly referred to as simply ‘zk’, is an area of cryptography that has drawn significant interest over the past several years. Once a niche area of research for a small coterie of academics and engineers, zk has blossomed into a diverse development sector attracting both venture capital and talent.
But how does zk actually function? Observers are quick to grasp the potential privacy benefits brought about by zk applications, but few understand the engineering that makes it possible.
In this edition of Full Stack, we'll delve into the concept of zkSNARK (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge), potential applications of this technology, and the security issues that must be addressed by zk developers.
(Want help with your ZK or MPC project? Reach out to a member of the team here!)
Introduction
In short, zero-knowledge proofs enable users to demonstrate their knowledge or possession of information without revealing any specifics.
This is achieved using a cryptographic technique where one party - the ‘Prover’ - attempts to prove that they have specific knowledge to another party - the ‘Verifier’.
A zkSNARK is a concise method of zero-knowledge proof, and must satisfy three conditions to function:
Completeness: Given a statement and a witness, the Prover can convince the Verifier.
Soundness: A malicious Prover cannot convince a Verifier of a false statement.
Zero-Knowledge: The proof does not reveal anything other than the truth of the statement, and in particular does not reveal the Verifier's witnesses.
How zkSNARK can be practically applied
The potential applications for zkSNARKs are very broad, but here are some of the main use cases:
Privacy Transactions: Privacy transaction platforms like Zcash and Tornado Cash use zkSNARKs to protect transactions, keeping transaction details (such as sender, receiver, and transaction amount) private from external observers.
Lightweight Blockchain Verification: Nodes can use zkSNARKs to verify the validity of a large number of transactions without checking the details of each transaction, reducing the computational requirements for verification.
Privacy-Preserving Computation: This allows the computation of encrypted data, providing only the result of the computation and a proof of its correctness without revealing the original data.
Secure Data Sharing: A zkSNARK allows data owners to share specific data attributes with third parties, such as specific statistical information from a dataset, without revealing the entire dataset.
Existing zkSNARK protocols
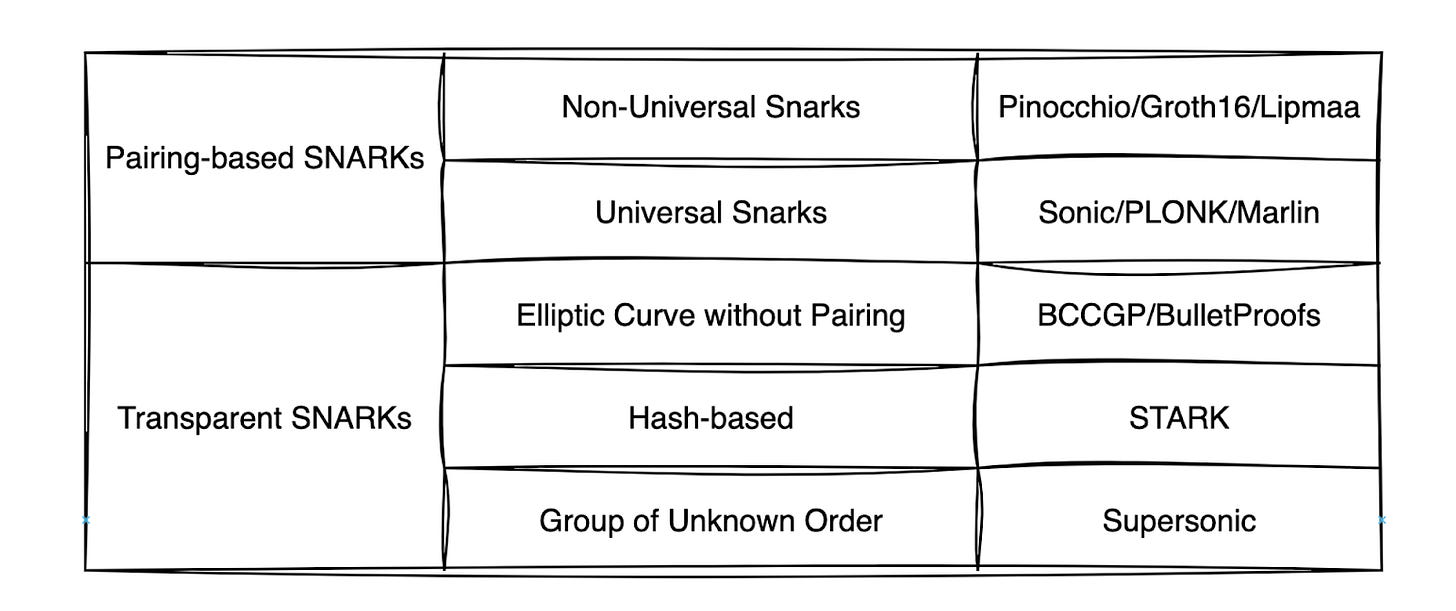
The common zkSNARK protocols fall into two main categories:
Pairing-based SNARKs: Pairing-based SNARKs are protocols based on elliptic curve pairing. These construct “multiplicative homomorphism-like” operations based on elliptic curves. Pairing-based SNARKs are further divided into Non-Universal, such as Pinocchio, Groth16, and Lipmaa, and Universal, like Sonic, PLONK, and Marlin.
Transparent SNARKs: Transparent SNARKs do not require a trusted setup globally. Based on the construction foundation, transparent SNARKs can be further classified into categories such as Elliptic Curves without Pairing, Hash-based zkSNARKs, and Groups of Unknown Order.
Groth16
Groth16 is a zero-knowledge proof system built on the mathematical foundations of elliptic curve cryptography and abstract algebra, which have practical applications in many fields. The Groth16 proof system is characterized by efficient performance and short proofs.
The transformation process of zkSNARK in the generation process is as follows. There is a FUNCTION for which generating a zero-knowledge proof requires the following steps:
Problem transformation: NP problem → circuit → R1CS → QAP
R1CS (Rank-1 Constraint Systems): During the construction of Groth16, the problem is converted into a gate circuit, which can be further represented in the format of R1CS. R1CS constraints are usually expressed using formulas of the following form: Az * Bz = C*z.
QAP: QAP is used to represent computational problems as relationships between polynomials in the form:$\sum_{i=0}^m a_i\times l_i(x) \cdot \sum_{i=0}^m a_i\times r_i(x)- \sum_{i=0}^m a_i\times w_i(x)=t(x)h(x)$, where $t(x)=(x-1)(x-2)...(x-n)$
Prove that the QAP equation holds (completeness+soundness)
Add a zero-knowledge realization on top of that
Plonk
The Plonk algorithm implements a Universal zero-knowledge proof, and the initial setup is required only once. The circuit under the Plonk algorithm consists of either an addition gate or a multiplication gate.
The constraint system constrains two logics:
Constraints hold for each gate
Each gate in plonk can be represented by the following polynomials:
$(q_L)i · x{ai} + (q_R)i · x{bi} + (q_O)i · x{ci} + (q_M)i · (x{ai}x_{bi} ) + (q_C)_i = 0$
Different assignments to $q_L,q_R,q_O,q_M,q_C$ can represent different gate operations.
Copy constraints: Ensuring the wire shared by gate and gate is correct
Plonk adds a new mapping polynomial to the same original polynomial. The copy-constraint of polynomials can be determined by verifying the concatenation between the two polynomials.
Halo2
Halo2 is a zkSNARK module applied to Zcash. A recursive proof is used in Halo/Halo2 for aggregation of proof content, as well as an Inner Product Argument (IPA) based on the BulletProof algorithm.
The part of the circuit in Halo2 is modified based on Plonk. In Halo2, you can use its corresponding API to define the gate, layout, and design the circuit.
Security issues in zkSNARK
Protocol issues
Security issues with the protocol itself may make upper-layer applications that use this protocol vulnerable.
For example, Groth16 was revealed to have a number of known attacks, and Groth's proof process is as follows:
Prover calculate(A,B,C):
Meanwhile, the Verifier verifies an equation:
When there is an overlap between Prover's Witness and the part of the statement, the Prover can utilize Groth16's malleability attack to construct against proof, such as constructing to cause effects such as double-flower attacks.
Circuit issues
An important part of building zkSNARK is to build circuits that generate the necessary proofs. These can be built using the Circom circuit language or Halo2, among others.
There are a number of problems that may exist during the construction of a circuit, including:
Under/Over Constraints
Missing range check
Overflow/Underflow
Logic problems in circuits, etc.
Other issues
In the implementation of zkSNARK protocols or circuits, there may be certain project-specific security issues.
For instance, within zkSNARK protocols, the transition from interactive proofs to non-interactive proofs using the Fiat-Shamir transform can introduce risks to the security of the protocol. An issue in the Fiat-Shamir transform process could allow an attacker to construct unintended proofs that pass verification, thereby compromising the soundness of the protocol (e.g. Frozen Heart vulnerability, Linea ‘Last Challenge’ vulnerability).
Summary
zkSNARK has advanced the fields of cryptography and privacy protection, and provides powerful tools for building secure and efficient decentralized systems; it is a disruptive technology that could play a key role in the evolution of decentralized applications. However, it also carries unique security issues, which must be addressed for zk applications to scale.